The law of the excluded muddle
In the second half of the nineteenth century and the early part of the twentieth there was a realisation that sometimes a mathematical proof showing the existence of something didn't actually show how to construct it. Some people took exception to such
nonconstructive proofs, and there is now a branch of mathematics which concentrates exclusively on constructive proofs. In accounts of constructive mathematics, the central question is often said to be the acceptance of the law of the excluded middle. If I can show that not-X is false (leads to a contradiction) then have I proved X? However, I don't see this as central to the matter, rather I see it going back to the older philosophical question of belief in
actual infinities.
The merely difficult we do immediately...
There does seem to be some confusion in the matter, since mathematical proofs are often use such
reductio ad absurdum, when they could just as well be cast as constructive proofs (establishing a contradiction usually leads to a shorter proof). Given a number N, Euclid tells us that
P=
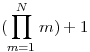
will have a prime factor larger than N. So if you want a prime number larger than N, you just need to look at the factors of P. If you want the next prime after N, you need to check each number in turn, but Euclid's proof does tell us that this procedure will terminate. So is Euclid's proof constructive or not? Well it doesn't offer a shorter way of finding the next prime than the brute force approach, but who said constructivism was about finding faster algorithms? Likewise for games such as
Hex,
John Nash gave a nonconstructive proof that the first player has a winning strategy, but of course he would have already known how to find the winning strategy - the brute force approach of constructing the game tree. This might not be possible in practice, but so what?
Actually infinite
In the case of the prime numbers Euclid's proof shows that there are an infinite number of primes. In this sense it might be said to be non-constructive, since it doesn't give the whole set 'at once'. But here the problem is really within the question - it is hard to see how any proof that a set is infinite would be immune to such objections. Euclid showed that the primes never run out - that they are potentially infinite. The possibility of potential versus actual infinities was debated for a long time by philosophers and mathematicians, but following the work of
Georg Cantor, actually infinite sets came to be considered respectable by most mathematicians. An example of the sort of nonconstructive proof which became acceptable in this way is that of the
Hilbert basis theorem (If a commutative ring R is Noetherian then so is the ring of polynomials over R), of which
Paul Gordan said:"This isn't mathematics, it is theology!". But here again, if you look into the proof then the problem appears in dealing with infinite sets which are a part of the way the theorem is stated (a constructive proof is possible if it is stated in a different way).
Existence?
When we talk of the number 2 it is fairly clear what is meant - we can point to sets of two objects. However, it is also possible to define 2 from the axioms of arithmetic as the successor of 1. In the case of other mathematical objects the axiomatic definition may be all we have, and in this case the existence of such objects may be called into question. Pythagoras didn't like the idea of the irrational numbers, and even
Kronecker, an influential mathematician in the nineteenth century, sometimes denied their existence. However, most of us accept the existence of √2, and so would see the proof of its irrationality of as a constructive proof of the existence of irrationals. Cantor's proof of the existence of transcendental numbers is sometimes thought to be non-constructive, but if you accept that an algorithm for generating a sequence of decimal digits defines a real number then Cantor's proof is certainly constructive. But here we run into a problem - not every real number has such a definition (there are uncountably many real numbers, and only countably many possible algorithms). It is those numbers which we can't describe whose existence may be called into question - do we just think of them as being 'out there' in some sense. Note that talking about countable sets can generally be put in the form of potential infinities (e.g a potential infinity of possible algorithms), whereas uncountable sets definitely require the belief in actual infinities.
The axiom of choice claims the existence of a choice function f choosing one element out of each set S in a collection C of nonempty sets. Proofs which use the axiom of choice are prime examples of nonconstructive proofs (as they don't give a description of how to calculate f). However, here again there is a problem. If you are a true constructivist then you don't think of infinite sets as being 'out there' in some sense, so S and C are just symbols. However, then the choice function f has much the same status as 2 being defined axiomatically as the successor of 1, and so you can't complain about it not being properly defined.
Really nonconstructive
Since the many examples are seen to have problems, the following has been given as an example of a nonconstructive proof. To prove that there exist irrational numbers a and b such that b
a is rational, consider (√2
√2)
√2=2. Take a=√2. Now either √2
√2 is rational, in which case b=√2 or else it is irrational which case b=√2
√2, but the proof doesn't determine which. Well I agree that this is a nonconstructive proof, but it's hardly the stuff of 'theology', which brings me back to my claim that the law of the excluded middle isn't the main issue in nonconstructive proofs.
My belief is that the issue will eventually become part of the question of computability. Given a computer program, either it halts or it doesn't but there is no general procedure for finding out which. This leads to Chaitin's constant - the probability that a random computer program will halt - which can be thought of as a genuinely non-constructable number. I would see theorems such as Hilbert's basis theorem as being subject to the same sort of analysis - showing that there is no general procedure for constructing what is claimed to exist, without worrying about whether you believe the law of the excluded middle or in Platonic notions of infinite sets as being 'out there' in some way
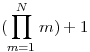 will have a prime factor larger than N. So if you want a prime number larger than N, you just need to look at the factors of P. If you want the next prime after N, you need to check each number in turn, but Euclid's proof does tell us that this procedure will terminate. So is Euclid's proof constructive or not? Well it doesn't offer a shorter way of finding the next prime than the brute force approach, but who said constructivism was about finding faster algorithms? Likewise for games such as Hex, John Nash gave a nonconstructive proof that the first player has a winning strategy, but of course he would have already known how to find the winning strategy - the brute force approach of constructing the game tree. This might not be possible in practice, but so what?
will have a prime factor larger than N. So if you want a prime number larger than N, you just need to look at the factors of P. If you want the next prime after N, you need to check each number in turn, but Euclid's proof does tell us that this procedure will terminate. So is Euclid's proof constructive or not? Well it doesn't offer a shorter way of finding the next prime than the brute force approach, but who said constructivism was about finding faster algorithms? Likewise for games such as Hex, John Nash gave a nonconstructive proof that the first player has a winning strategy, but of course he would have already known how to find the winning strategy - the brute force approach of constructing the game tree. This might not be possible in practice, but so what?

